LeetCode热题100:链表
摘要
相交链表
给你两个单链表的头节点 headA 和 headB
,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回
null 。
图示两个链表在节点 c1 开始相交:
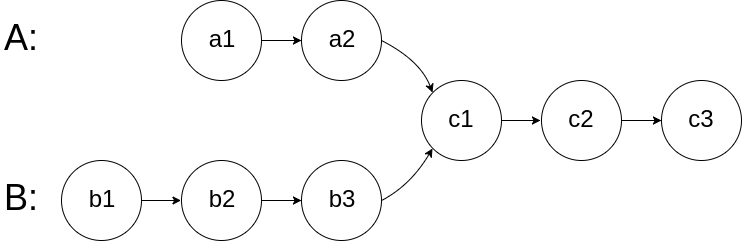
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须
保持其原始结构 。
双指针O(M+N):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public:
ListNode *getIntersectionNode(ListNode *h1, ListNode *h2) {
ListNode *p1 = h1, *p2 = h2;
while(p1 != p2){
p1 = p1 == nullptr ? h2 : p1->next;
p2 = p2 == nullptr ? h1 : p2->next;
}
return p1;
}
};
|
反转链表
给你单链表的头节点 head
,请你反转链表,并返回反转后的链表。
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public:
ListNode* reverseList(ListNode* h) {
ListNode* pre = nullptr;
while(h){
ListNode *nex = h->next;
h->next = pre;
pre = h;
h = nex;
}
return pre;
}
};
|
回文链表
给你一个单链表的头节点 head
,请你判断该链表是否为回文链表。如果是,返回 true
;否则,返回 false 。
1)转成数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
bool isPalindrome(ListNode* h) {
vector<int > v;
while(h != nullptr){
v.push_back(h->val);
h = h->next;
}
for(int i = 0 ; i < v.size()/2 ; i ++){
if(v[i] != v[v.size()-1-i]) return false;
}
return true;
}
};
|
2)快慢指针 + 链表反转
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| class Solution {
public:
ListNode* middleNode(ListNode *h){
ListNode *s = h, *f = h;
while(f != nullptr && f->next != nullptr){
s = s->next;
f = f->next->next;
}
return s;
}
ListNode* reverseList(ListNode *h){
ListNode *pre = nullptr;
while(h){
ListNode * nex = h->next;
h->next = pre;
pre = h;
h = nex;
}
return pre;
}
bool isPalindrome(ListNode* h) {
ListNode *mid = middleNode(h);
ListNode *b = reverseList(mid);
while(b){
if(b->val != h->val) return false;
b = b->next;
h = h->next;
}
return true;
}
};
|
环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next
指针再次到达,则链表中存在环。
为了表示给定链表中的环,评测系统内部使用整数 pos
来表示链表尾连接到链表中的位置(索引从 0
开始)。注意:pos 不作为参数进行传递
。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回
false 。
1)哈希
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public:
bool hasCycle(ListNode *h) {
unordered_set<ListNode*> st;
while(h != nullptr){
st.insert(h);
if(st.count(h->next)){
return true;
}
h = h->next;
}
return false;
}
};
|
2)快慢指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
bool hasCycle(ListNode *h) {
ListNode *s = h, *f = h;
while(f && f->next){
s = s->next;
f = f->next->next;
if(s == f) return true;
}
return false;
}
};
|
环形链表 II
给定一个链表的头节点 head
,返回链表开始入环的第一个节点。 如果链表无环,则返回
null。
如果链表中有某个节点,可以通过连续跟踪 next
指针再次到达,则链表中存在环。
为了表示给定链表中的环,评测系统内部使用整数 pos
来表示链表尾连接到链表中的位置(索引从 0 开始)。如果
pos 是
-1,则在该链表中没有环。注意:pos
不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
1)哈希
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
ListNode *detectCycle(ListNode *h) {
unordered_set<ListNode*> st;
while(h != nullptr){
st.insert(h);
if(st.count(h->next)){
return h->next;
}
h = h->next;
}
return nullptr;
}
};
|
2)快慢指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public:
ListNode *detectCycle(ListNode *h) {
ListNode *s = h, *f = h;
while(f && f->next){
s = s->next;
f = f->next->next;
if(s == f) break;
}
if(!(f && f->next)) return nullptr;
f = h;
while(s != f){
s = s->next;
f = f->next;
}
return f;
}
};
|
合并两个有序链表
将两个升序链表合并为一个新的 升序
链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
1)递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
ListNode* mergeTwoLists(ListNode* h1, ListNode* h2) {
if(h1 == nullptr) return h2;
if(h2 == nullptr) return h1;
if(h1->val < h2->val){
h1->next = mergeTwoLists(h1->next, h2);
return h1;
}else{
h2->next = mergeTwoLists(h2->next, h1);
return h2;
}
}
};
|
2)非递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
ListNode* mergeTwoLists(ListNode* h1, ListNode* h2) {
ListNode* h3 = new ListNode();
ListNode* pre = h3;
while(h1 && h2){
if(h1->val < h2->val){
pre->next = h1;
h1 = h1->next;
}else{
pre->next = h2;
h2 = h2->next;
}
pre = pre->next;
}
while(h1){
pre->next = h1;
h1 = h1->next;
pre = pre->next;
}
while(h2){
pre->next = h2;
h2 = h2->next;
pre = pre->next;
}
return h3->next;
}
};
|
两数相加
给你两个 非空
的链表,表示两个非负的整数。它们每位数字都是按照 逆序
的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public:
ListNode* addTwoNumbers(ListNode* h1, ListNode* h2) {
ListNode *t1 = h1, *t2 = h2;
while(t1->next || t2->next){
if(t1->next == nullptr){
t1->next = new ListNode(0, nullptr);
}else if(t2->next == nullptr){
t2->next = new ListNode(0, nullptr);
}
t1 = t1->next; t2 = t2->next;
}
t1 = h1, t2 = h2;
while(t1 && t2){
int x = t1->val;
int y = t2->val;
t1->val = (x+y) % 10;
int add = (x+y) / 10;
if(add){
if(t1->next) t1->next->val += add;
else t1->next = new ListNode(add);
}
t1 = t1->next;
t2 = t2->next;
}
return h1;
}
};
|
删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n
个结点,并且返回链表的头结点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public:
ListNode* removeNthFromEnd(ListNode* h, int n) {
ListNode *t = h;
int len = 0;
while(t){
t = t->next;
len++;
}
ListNode *pre = nullptr, *nex = nullptr;
t = h;
for(int i = 1 ; i <= len-n ; i ++){
pre = t;
t = t->next;
nex = t->next;
}
if(n == len){
h = h->next;
}else{
pre->next = nex;
}
return h;
}
};
|
两两交换链表中的节点
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
1)修改值
1
2
3
4
5
6
7
8
9
10
11
| class Solution {
public:
ListNode* swapPairs(ListNode* h) {
ListNode *t = h;
while(t && t->next){
swap(t->val, t->next->val);
t = t->next->next;
}
return h;
}
};
|
2)不修改值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
ListNode* swapPairs(ListNode* h) {
if(!(h && h->next)) return h;
ListNode *dum = new ListNode(0, h);
ListNode *p = dum;
while(p->next && p->next->next){
ListNode *l = p->next;
ListNode *r = p->next->next;
l->next = r->next;
r->next = l;
p->next = r;
p = l;
}
return dum->next;
}
};
|
K 个一组翻转链表
给你链表的头节点 head ,每 k
个节点一组进行翻转,请你返回修改后的链表。
k
是一个正整数,它的值小于或等于链表的长度。如果节点总数不是
k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public:
void reverseList(ListNode *s, ListNode *e){
ListNode *pre = nullptr;
while(s != e){
ListNode *nex = s->next;
s->next = pre;
pre = s;
s = nex;
}
e->next = pre;
}
ListNode* reverseKGroup(ListNode* h, int k) {
ListNode *dum = new ListNode(0, h);
ListNode *l = dum;
while(l){
ListNode *r = l;
for(int i = 1 ; r && i <= k ; i ++){
r = r->next;
}
if(r == nullptr) break;
ListNode *nex_l = l->next;
ListNode *nex = r->next;
ListNode *pre = l;
reverseList(l->next, r);
pre->next = r;
nex_l->next = nex;
l = nex_l;
}
end: return dum->next;
}
};
|
随机链表的复制
给你一个长度为 n
的链表,每个节点包含一个额外增加的随机指针 random
,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。
深拷贝应该正好由 n 个 全新
节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的
next 指针和 random
指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点
。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public:
Node* copyRandomList(Node* h) {
unordered_map<Node*, Node*> mp;
Node *t = h;
Node *dum = new Node(0), *pre = dum;
while(t){
Node * node = new Node(t->val);
node->random = t->random;
pre->next = node;
pre = node;
mp[t] = node;
t = t->next;
}
Node * tt = dum->next;
while(tt){
tt->random = mp[tt->random];
tt = tt->next;
}
return dum->next;
}
};
|
排序链表
给你链表的头结点 head ,请将其按 升序
排列并返回 排序后的链表 。
1)转成数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public:
ListNode* sortList(ListNode* h) {
vector<int > v;
ListNode *dum = new ListNode(0, nullptr);
while(h){
v.push_back(h->val);
h = h->next;
}
sort(v.begin(), v.end());
ListNode * pre = dum;
for(auto it : v){
ListNode * node = new ListNode(it);
pre->next = node;
pre = node;
}
return dum->next;
}
};
|
2)归并排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public:
ListNode* sortList(ListNode* h) {
if(!(h && h->next)) return h;
ListNode *mid = findMid(h);
ListNode *newh = mid->next;
mid->next = nullptr;
ListNode *l = sortList(h);
ListNode *r = sortList(newh);
return merge(l, r);
}
ListNode* findMid(ListNode* h){
ListNode *s = h, *f = h;
while(f->next && f->next->next){
s = s->next;
f = f->next->next;
}
return s;
}
ListNode* merge(ListNode *h1, ListNode *h2){
if(!h1) return h2;
if(!h2) return h1;
if(h1->val < h2->val){
h1->next = merge(h1->next, h2);
return h1;
}else{
h2->next = merge(h1, h2->next);
return h2;
}
}
};
|
合并 K 个升序链表
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
ListNode *dum = new ListNode(0, nullptr), *pre = dum;
priority_queue<pair<int,ListNode*>, vector<pair<int,ListNode*> >, greater<pair<int,ListNode*> > > pq;
for(int i = 0 ; i < lists.size() ; i ++){
if(lists[i]) pq.push({lists[i]->val, lists[i]});
}
while(!pq.empty()){
ListNode *f = pq.top().second;
pq.pop();
if(f->next) pq.push({f->next->val, f->next});
pre->next = f;
pre = f;
}
return dum->next;
}
};
|
LRU 缓存
请你设计并实现一个满足 LRU
(最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数
作为容量 capacity 初始化 LRU 缓存int get(int key) 如果关键字 key
存在于缓存中,则返回关键字的值,否则返回 -1 。void put(int key, int value) 如果关键字
key 已经存在,则变更其数据值 value
;如果不存在,则向缓存中插入该组 key-value
。如果插入操作导致关键字数量超过 capacity ,则应该
逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1)
的平均时间复杂度运行。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
struct Node{
int key, val;
Node *next, *pre;
Node(int key_ = 0, int val_ = 0, Node *next_ = nullptr, Node *pre_ = nullptr){
key = key_;
val = val_;
next = next_;
pre = pre_;
}
};
class LRUCache {
public:
unordered_map<int, Node*> mp;
Node *dum;
int siz;
void remove(Node *p){
p->pre->next = p->next;
p->next->pre = p->pre;
}
void push_front(Node *p){
p->pre = dum;
p->next = dum->next;
dum->next->pre = p;
dum->next = p;
}
LRUCache(int capacity) {
siz = capacity;
mp.clear();
dum = new Node();
dum->next = dum;
dum->pre = dum;
}
int get(int key) {
if(mp.count(key)){
Node* p = mp[key];
remove(p);
push_front(p);
return p->val;
}
return -1;
}
void put(int key, int value) {
if(mp.count(key)){
Node *p = mp[key];
remove(p);
push_front(p);
p->val = value;
}else{
Node *p = new Node(key, value, nullptr, nullptr);
mp[key] = p;
push_front(p);
if(mp.size() > siz){
Node *back = dum->pre;
mp.erase(back->key);
remove(back);
}
}
}
};
|
