AcWing算法提高课：动态规划5-状态压缩DP

摘要

1064. 小国王 - AcWing题库：状态压缩DP 求方案数【棋盘】【限制放置个数】

327. 玉米田 - AcWing题库：状态压缩DP 求方案数【棋盘】【存在无效点】

292. 炮兵阵地 - AcWing题库：状态压缩DP 求方案数【棋盘】【需要考虑前2行 / 列】

524. 愤怒的小鸟 - AcWing题库：状态压缩DP + 计算几何【重复覆盖问题】

529. 宝藏 - AcWing题库：状态压缩DP + 最小生成树

1064 小国王

在 n×n 的棋盘上放 k 个国王，国王可攻击相邻的 8 个格子，求使它们无法互相攻击的方案总数。

题解

经典状态压缩DP问题；

首先，我们每行的每种合法状态存入sit数组，并将该状态下的国王数存入tol数组；

然后，设置状态转移方程为： \[ dp[i][j][k]=dp[i][j][k]+dp[i-1][r][k-tol[j]] \quad if \space check(j,r)==true \] i为当前行，k为已放置的国王数，j 和 r分别为当前行 和 上一行的状态下标。若两个状态不冲突，进行累加；

最后，合并所有\(dp[n][i]\)，得到总方案数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
using namespace std;
const int maxn = 11;

int n,k,cnt,ans;
int sit[(1<<maxn)],tol[(1<<maxn)],dp[maxn][(1<<maxn)][maxn*maxn];

bool check(int a, int b){
	if(sit[a] & sit[b]) return false;
	if((sit[a]<<1) & sit[b]) return false;
	if((sit[a]>>1) & sit[b]) return false;
	return true;
}

int main(void){
	cin>>n>>k;
	// init state
	for(int s = 0 ; s < (1<<n) ; s ++){
		if(!(s & s >> 1)){
			sit[++cnt] = s;
			for(int i = 0 ; i < n ; i ++){
				if((s >> i) & 1) tol[cnt]++;
			}
		}
	}
	dp[0][1][0] = 1;
	for(int i = 1 ; i <= n ; i ++){
		for(int j = 1 ; j <= cnt ; j ++){
			for(int r = 1 ; r <= cnt ; r ++){
				if(check(j,r)){
					for(int c = k; c >= tol[j] ; c --){
						dp[i][j][c] += dp[i-1][r][c-tol[j]];
					}
				}
			}
		}
	}
	for(int i = 1 ; i <= cnt ; i ++){
		ans += dp[n][i][k];
	}
	cout<<ans;
	return 0;
}

327 玉米田

玉米田由 M×N 个小土地方格组成。

部分土地是不育的，无法种植。相邻的土地也不能同时种植玉米，也就是说种植玉米的所有方格之间都不会有公共边缘。

求出共有多少种种植方法。

注意：土地上什么都不种也算一种方法。

题解

该题在1064的基础上增加了“不合法的方格”，但没有放置数量限制，所以dp数组可以减少一个维度。

首先，我们每行的种土豆的合法状态存入sit数组；

然后，设置状态转移方程为： \[ dp[i][j] = dp[i][j] + dp[i-1][r] \quad if \space check(j,r) == true \\ \] i为当前行，j 和 r分别为当前行 和 上一行的状态下标。若两个状态不冲突，进行累加；【为了判断不合法的方格，使用vis数组存储01状态】

最后，合并所有\(dp[m][i]\)，得到总方案数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<bits/stdc++.h>
using namespace std;
const int mod = 1e8;
const int maxm = 200;
const int maxn = 13;

int m,n,cnt,ans;
int sit[(1<<maxn)];
int dp[maxm][(1<<maxn)], vis[maxm];

int main(void){
	cin>>m>>n;
	for(int i = 1 ; i <= m ; i ++){
		for(int j = 1 ; j <= n ; j ++){
			int f;cin>>f;
			vis[i] = vis[i]|(f<<(j-1));
		}
	}
	// init state
	for(int s = 0 ; s < (1<<n) ; s ++){
		if(!(s & s>>1)){
			sit[++cnt] = s;
		}
	}
	dp[0][1] = 1;
	for(int i = 1 ; i <= m ; i ++){
		for(int j = 1 ; j <= cnt ; j ++){
			for(int r = 1 ; r <= cnt ; r ++){
                // check
				if( (~vis[i])& sit[j] ) continue;
				if( sit[j] & sit[r] ) continue;
				dp[i][j] = (dp[i][j] + dp[i-1][r])%mod;
			}
		}
	}
	for(int i = 1 ; i <= cnt ; i ++){
		ans = (ans + dp[m][i])%mod;
	}
	cout<<ans;
	return 0;
}

292 炮兵阵地

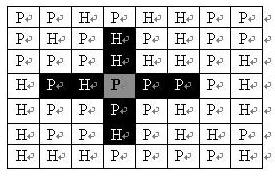
一个 N×M 的地图由 N 行 M 列组成，地图的每一格可能是山地（用 H 表示），也可能是平原（用 P 表示）。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

炮兵的攻击范围不受地形的影响。求最多能够摆放多少个炮兵部队。

题解

该题和1064、327的区别在于，状态是否合法需要分析前2行，所以在dp数组需要同时存储2行的状态。

此外，这道题不是要求方案数，而是求炮兵部队的数量最大值。

设置状态转移方程为： \[ dp[i][j][k] = max(dp[i][j][k], dp[i-1][r][k] + tol[j]) \quad if \space check(j,r,k) == true \] i为当前行，j 、r、k分别为当前行 、上一行、再上一行的状态下标。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;
const int maxn = 105;
const int max_cnt = 100;

// 这里如果直接开(1<<maxn)会Memory Limit
// 1<<10 = 1024
// 通过估算，得到最大max_cnt < 100 [if m = 10, PPPPPPPPPP];

int n,m,cnt,ans;
int tol[max_cnt];
int vis[maxn],sit[max_cnt],dp[maxn][max_cnt][max_cnt];

int main(void){
	cin>>n>>m;
	for(int i = 1 ; i <= n ; i ++){
		for(int j = 1 ; j <= m ; j ++){
			char c;cin>>c;
			if(c == 'P') vis[i] = vis[i]|(1<<(j-1));
		}
	}
	// init state
	for(int s = 0 ; s < (1<<m) ; s ++){
		if( !( s & (s>>1) ) && !(s & (s>>2) ) ){
			sit[++cnt] = s;
			for(int i = 0 ; i < m ; i ++){
				if((s>>i) & 1) tol[cnt]++;
			}
		}
	}
	for(int i = 1 ; i <= n ; i ++){
		for(int j = 1 ; j <= cnt ; j ++){
			for(int r = 1 ; r <= cnt ; r ++){
				for(int k = 1 ; k <= cnt ; k ++){
					if((~vis[i]) & sit[j]) continue;
					if(sit[j] & sit[r]) continue;
					if(sit[j] & sit[k]) continue;
					dp[i][j][r] = max(dp[i][j][r], dp[i-1][r][k] + tol[j]);
					ans = max(dp[i][j][r],ans);
				}
			}
		}
	}
	cout<<ans;
	return 0;
}

524 愤怒的小鸟

有一架弹弓位于 (0,0) 处，每次 Kiana 可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如 y=ax2+bx 的曲线。在游戏的某个关卡里，平面的第一象限中有 n 只绿色的小猪，其中第 i 只小猪所在的坐标为 (xi,yi)。

这款游戏一共有 T 个关卡，求每个关卡中，消灭所有小猪最少需要的小鸟数量。

题解

首先，我们进行预处理，只需要枚举所有不重合的点，每2点可以确定一条过原点的抛物线。 \[ \left.\left\{\begin{array}{c}y_1=ax_1^2+bx_1\\y_2=ax_2^2+bx_2\end{array}\right.\right.\quad\Rightarrow\quad\left\{\begin{array}{c}a=\frac{\frac{y_1}{x_1}-\frac{y_2}{x_2}}{x_1-x_2}\\b=\frac{y_1}{x_1}-ax_1\end{array}\right. \] 接着，枚举每个小猪是否在某条抛物线上，我们就得到了每个抛物线的01状态，即能消灭哪些小猪，并存在sit数组中；

然后，我们把这个问题转化为 重复覆盖问题。状态转移方程为： \[ dp[s|sit[i][j]] = min(dp[s|sit[i][j]], dp[s] + 1) \] 这里 i 和 j 分别表示2点，sit为它们确定的抛物线的01状态。

最后，得到结果为最少抛物线数为\(dp[(1<<n)-1]\)。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<bits/stdc++.h>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 19; 

struct Point{
	double x,y;
}p[maxn];

int n,m,t,cnt;
int sit[maxn][maxn], dp[1<<maxn];

bool equal(double a, double b){
	return fabs(a - b) < 1e-6;
}

void init_sit(){
	memset(sit,0,sizeof(sit));
	for(int i = 1 ; i <= n ; i ++){
		sit[i][i] = 1<<(i-1);
		for(int j = 1 ; j <= n ; j ++){
			double x1,y1,x2,y2;
			x1 = p[i].x; y1 = p[i].y;
			x2 = p[j].x; y2 = p[j].y;
			if(equal(x1, x2)) continue; // x1 - x2 != 0
			double a = (y1 / x1 - y2 / x2) / (x1 - x2); 
			double b = (y1 / x1) - a * x1;
			if(equal(a,0.0) || a > 0) continue; // a < 0
			for(int k = 1 ; k <= n ; k ++){
				if(equal(a*p[k].x*p[k].x + b*p[k].x, p[k].y)){
					sit[i][j] = sit[i][j] | (1<<(k-1));
				}
			}
		}
	}
}

void solve(){
	cin.tie(0),cout.tie(0),ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i = 1 ; i <= n ; i ++){
		cin>>p[i].x>>p[i].y;
	}
	init_sit();
	memset(dp,inf,sizeof(dp));
	dp[0] = 0;
	for(int i = 1 ; i <= n ; i ++){
		for(int j = i ; j <= n ; j ++){
			for(int s = 0 ; s < (1<<n) ; s ++){
				dp[s|sit[i][j]] = min(dp[s|sit[i][j]], dp[s] + 1);
			}
		}
	}
	cout<<dp[(1<<n)-1]<<"\n";
}

int main(void){
	cin>>t;
	while(t--){
		solve();
	}
	return 0;
}
题解 > AcWing > 动态规划
#动态规划 #AcWing
AcWing算法提高课：动态规划5-状态压缩DP
https://czwcugb.github.io/题解/acwing-advance/AcWing-DP-5/
作者
ChenZhiwei
发布于
2025年2月10日
许可协议