AcWing算法提高课：动态规划3-背包模型

摘要

423. 采药 - AcWing题库：01背包模板题-1

426. 开心的金明 - AcWing题库：01背包模板题-2

1024. 装箱问题 - AcWing题库：01背包变形，只给体积，求占用背包空间的最大值

278. 数字组合 - AcWing题库：求体积恰好为m的01背包方案数

1023. 买书 - AcWing题库：体积恰好为m的01背包方案数（完全背包）-1

1021. 货币系统 - AcWing题库：体积恰好为m的01背包方案数（完全背包）-2

532. 货币系统 - AcWing题库：完全背包，求解极大线性无关组

1019. 庆功会 - AcWing题库：多重背包的二进制优化

6. 多重背包问题 III - AcWing题库：多重背包的单调队列优化

7. 混合背包问题 - AcWing题库：混合背包 <=> 包含完全背包情况的多重背包

8. 二维费用的背包问题 - AcWing题库：二维01背包

1022. 宠物小精灵之收服 - AcWing题库：二维01背包+输出最优解下的状态（条件2）

1020. 潜水员 - AcWing题库：二维背包（至少大于n和m条件）

1013. 机器分配 - AcWing题库：分组背包问题+状态回溯

487. 金明的预算方案 - AcWing题库：分组背包 + 二进制枚举分组内选择

10. 有依赖的背包问题 - AcWing题库：树上背包

11. 背包问题求方案数 - AcWing题库：01背包求最优解的方案数

12. 背包问题求具体方案 - AcWing题库：01背包求字典序最小的具体方案

734. 能量石 - AcWing题库：01背包 + 贪心[邻项交换]（价值随时间减少）

423 采药

给n个物品，每个物品有对应的体积和价值，求不超过背包体积m，最多获得的价值。

题解

01背包模板题

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2000;

int n,m;
int w[maxn],v[maxn];
int dp[maxn];

int main(void){
	cin>>m>>n;
	for(int i = 1 ; i <= n ; i ++){
		cin>>w[i]>>v[i];
	}
	for(int i = 1 ; i <= n ; i ++){
		for(int j = m ; j >= w[i] ; j --){
			dp[j] = max(dp[j], dp[j-w[i]] + v[i]);
		}
	}
	cout<<dp[m];
	return 0;
}

426 开心的金明

给n个物品，每个物品有对应的价格和重要度，其价值 = 价格*重要度。

求不超过背包体积m的前提下，最多获得的价值。

题解

01背包模板题。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<bits/stdc++.h>
using namespace std;
const int maxm = 30050;

int n,m;
int dp[maxm];

int main(void){
	cin>>m>>n;
	for(int i = 1 ; i <= n ; i ++){
		int v,p;
		cin>>v>>p;
		for(int j = m ; j >= v ; j --){
			dp[j] = max(dp[j], dp[j-v] + v*p);
		}
	}
	cout<<dp[m];
	return 0;
}

1024 装箱问题

有一个箱子容量为 V，同时有 n 个物品，每个物品有一个体积（正整数）。

要求 n 个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。

题解

给n个不同体积的物品，放到总体积为m的箱子里，求最多占满的体积。

这里将初始值dp[0]设置为true，其他设置为false。

递归后可以知道：是否能填充到体积j（dp[j] == true）。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<bits/stdc++.h>
using namespace std;
const int maxn = 20050;

int n,m,ans,w[maxn];
bool dp[maxn];

int main(void){
	cin>>m>>n;
	for(int i = 1 ; i <= n ; i ++){
		cin>>w[i];
	}
	dp[0] = true;
	for(int i = 1 ; i <= n ; i ++){
		for(int j = m ; j >= w[i] ; j --){
			dp[j] = dp[j] | dp[j-w[i]];
			if(dp[j]) ans = max(ans, j);
		}
	}
	cout<<m-ans;
	return 0;
}

278 数字组合

给定 N 个正整数 A1,A2,…,AN，从中选出若干个数，使它们的和为 M，求有多少种选择方案。

题解

模板题 01背包求方案数

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<bits/stdc++.h>
using namespace std;
const int maxn = 105;
const int maxm = 10050;

int n,m;
int dp[maxm],a[maxn];

int main(void){
	cin>>n>>m;
	for(int i = 1 ; i <= n ; i ++){
		cin>>a[i];
	}
	dp[0] = 1;
	for(int i = 1 ; i <= n ; i ++){
		for(int j = m ; j >= a[i] ; j --){
			dp[j] = dp[j] + dp[j-a[i]];
		}
	}
	cout<<dp[m];
	return 0;
}

1023 买书

小明手里有n元钱全部用来买书，书的价格为10元，20元，50元，100元。

问小明有多少种买书方案？（每种书可购买多本）

题解

每种书可购买多本，意味着这是多重背包问题；

此外，注意这里题目说需要把n元钱花光，全部用来买书，所以0元的方案数为1，需要特判。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1050;

int n;
int a[5],dp[maxn];

int main(void){
	cin>>n;
	if(n == 0){
		cout<<1;
		return 0;
	}
	a[1] = 10; a[2] = 20; a[3] = 50; a[4] = 100;
	dp[0] = 1;
	for(int i = 1 ; i <= 4 ; i ++){
		for(int j = a[i] ; j <= n ; j ++){
			dp[j] = dp[j] + dp[j-a[i]];
		}
	}
	cout<<dp[n];
	return 0;
}

1021 货币系统

给你一个n种面值的货币系统，求组成面值为m的货币有多少种方案。

题解

多重01背包的方案数问题；

注意：这题结果数值较大，需要开Long Long；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const ll maxn = 20;
const ll maxm = 3050;

ll n,m;
ll a[maxn],dp[maxm];

int main(void){
	cin>>n>>m;
	if(n == 0){
		cout<<1;
		return 0;
	}
	for(int i = 1 ; i <= n ; i ++){
		cin>>a[i];
	}
	dp[0] = 1;
	for(int i = 1 ; i <= n ; i ++){
		for(int j = a[i] ; j <= m ; j ++){
			dp[j] = dp[j] + dp[j-a[i]];
		}
	}
	cout<<dp[m];
	return 0;
}

523 货币系统

共有 n 种不同面额的货币，第 i 种货币的面额为 a[i]，每一种货币都有无穷多张。

两个货币系统 (n,a)和 (m,b)是等价的，当且仅当对于任意非负整数 x，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。 

他们希望找到一个货币系统 (m,b)，满足 (m,b) 与原来的货币系统 (n,a)等价，且 m 尽可能的小。

题解

要求这道题的解，首先要知道极大线性无关组的概念：最大线性无关组 - 维基百科，自由的百科全书

货币系统\((n,a)\) ,如果存在\(a_j\)可以被\(a\)中其他的向量 线性表出： \[ a_j=\sum_{i\neq j}c_ia_i \]

则 \(a_j\) 在这个货币系统中是 无效的 (所有线性表示中需要用到\(a_j\)的项，都可以用\(\sum_i\neq jc_ia_i\) 代替) 因此，我们需要求出 货币系统\((n,a)\)的 最大无关向量组，即任意\(a_i\)都不能被其他向量 线性表出

由此，我们知道\((m,b)\)就是\((n,a)\)的极大线性无关组，使用完全背包模型，删去能用其他货币线性表示的无效货币，即可得到结果。

注意：这里需要进行排序，因为大面值的货币必须由小面值的货币组成。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<bits/stdc++.h>
using namespace std;
const int maxn = 105;

int t,n,m,a[maxn];
bool dp[maxn*25000];

void solve(){
	m = 0;
	memset(dp,false,sizeof(dp));
	cin>>n;
	for(int i = 1 ; i <= n ; i ++){
		cin>>a[i];
		m = max(a[i],m);
	}
	sort(a+1,a+1+n);
	dp[0] = true;
	int res = n;
	for(int i = 1 ; i <= n ; i ++){
		if(dp[a[i]]){
			res--;
			continue;
		}
		for(int j = a[i] ; j <= m ; j ++){
			dp[j] = dp[j] | dp[j-a[i]];
		}
	}
	cout<<res<<"\n";
	return;
}

int main(void){
	cin>>t;
	while(t--){
		solve();
	}
	return 0;
}

1019 庆功会

班主任决定开一场庆功会，为此拨款购买奖品犒劳运动员。每个奖品有对应的价格、价值（价格与价值是不同的概念）和能购买的最大数量（买0件到s件均可）。

给定拨款金额，求能买的最大价值。

题解

二进制优化的多重背包

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<bits/stdc++.h>
using namespace std;
const int maxm = 6050;

int n,m;
int dp[maxm];

int main(void){
	cin>>n>>m;
	for(int i = 1; i <= n ; i ++){
		int w,v,s;
		cin>>w>>v>>s;
		for(int k = 1 ; s > k ; s -= k, k += k){
			for(int j = m ; j >= k*w ; j --){
				dp[j] = max(dp[j], dp[j-k*w] + k*v);
			}
		}
		for(int j = m ; j >= s*w ; j --){
			dp[j] = max(dp[j], dp[j-s*w] + s*v);
		}
	}
	cout<<dp[m];
	return 0;
}

6 多重背包问题 III

有\(N\)种物品和一个容量是\(V\)的背包，第\(i\)种物品最多有\(s_i\)件，

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。

题解

参考：AcWing 6. 多重背包问题 III【单调队列优化+图示】 - AcWing

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1050;
const int maxm = 20050;

int n,m,tt,hh;
int w[maxn],v[maxn],s[maxn],q[maxm];
int dp[maxn][maxm];

int main(void){
	cin>>n>>m;
	for(int i = 1 ; i <= n ; i ++){
		cin>>w[i]>>v[i]>>s[i];
	}
	for(int i = 1 ; i <= n ; i ++){
		for(int r = 0 ; r < w[i] ; r ++){
			hh = 0;tt = -1;
			for(int j = r ; j <= m ; j += w[i]){
				while(hh <= tt && j - q[hh] > s[i]*w[i]) hh++;
				while(hh <= tt && dp[i-1][q[tt]] + (j-q[tt])/w[i]*v[i] < dp[i-1][j]) tt--;
				q[++tt] = j;
				dp[i][j] = dp[i-1][q[hh]] + (j-q[hh])/w[i]*v[i];
			}
		}
	}
	cout<<dp[n][m];
	return 0;
}

7 混合背包问题

有 N 种物品和一个容量是 V 的背包。物品一共有三类：

  • 第一类物品只能用1次（01背包）；
  • 第二类物品可以用无限次（完全背包）；
  • 第三类物品最多只能用 \(s_i\) 次（多重背包）；

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。

题解

01背包的情况可以当作 S == 1情况下的多重背包；

完全背包的情况，需要进行特判。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std;
const int maxm = 6050;

int n,m;
int dp[maxm];

int main(void){
	cin>>n>>m;
	for(int i = 1; i <= n ; i ++){
		int w,v,s;
		cin>>w>>v>>s;
		// 完全背包
		if(s == 0){
			for(int j = w; j <= m ; j ++){
				dp[j] = max(dp[j], dp[j-w] + v);
			}
			continue;
		}
		// 多重背包
		if(s == -1) s = 1;
		for(int k = 1 ; s > k ; s -= k, k += k){
			for(int j = m ; j >= k*w ; j --){
				dp[j] = max(dp[j], dp[j-k*w] + k*v);
			}
		}
		for(int j = m ; j >= s*w ; j --){
			dp[j] = max(dp[j], dp[j-s*w] + s*v);
		}
	}
	cout<<dp[m];	
	return 0;
}

8 二维费用背包问题

有\(N\)件物品和一个容量是\(V\)的背包，背包能承受的最大重量是\(M\) 。每件物品只能用一次。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量。

题解

相比普通的01背包，增加一个维度的状态，需要用二维数组存储，增加一层循环。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<bits/stdc++.h>
using namespace std;
const int maxt = 200;
const int maxm = 200;

int n,t,m;
int dp[maxt][maxm];

int main(void){
	cin>>n>>t>>m;
	for(int i = 1 ; i <= n ; i ++){
		int vo,w,v;
		cin>>vo>>w>>v;
		for(int j = t ; j >= vo ; j --){
			for(int k = m ; k >= w ; k --){
				dp[j][k] = max(dp[j][k], dp[j-vo][k-w] + v);
			}
		}
	}
	cout<<dp[t][m];
	return 0;
}

1022 宠物小精灵之收服

小智捕捉每个不同的精灵需要一定数量的精灵球，并消耗皮卡丘的体力值。他的目标是捕捉尽量多的精灵球。求 最多捕捉的精灵数 和 在该前提下最多剩余的体力。

题解

多条件的二维背包问题：精灵球和体力值分别代表dp值的两个状态，精灵数就是dp值。

满足二维背包条件的最优解可能有多个，这题要求我们分析在这些最优解（精灵数量最多）的状态，得到另一个解（精灵数量最多的情况下，最少消耗的体力为多少）。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1050;

int n,m,k;
int c[maxn],d[maxn],dp[maxn][maxn];
int ans1,ans2;

int main(void){
	cin>>n>>m>>k;
	for(int i = 1 ; i <= k ; i ++){
		cin>>c[i]>>d[i];
	}
	for(int i = 1 ; i <= k ; i ++){
		for(int j = n ; j >= c[i] ; j --){
			// 题目：使皮卡丘体力小于等于0的野生小精灵也不会被小智收服。
			// 所以这里r的最大值是m-1，不能取到m
			for(int r = m-1 ; r >= d[i] ; r --){ 
				dp[j][r] = max(dp[j][r], dp[j-c[i]][r-d[i]] + 1);
				if(dp[j][r] > ans1){
					ans1 = dp[j][r];
					//ans2 = r;
				}else if(dp[j][r] == ans1){
					//ans2 = min(ans2,r);
				}
			}
		}
	}
	// ans1 也可以单独求解
	// 即找到所有满足最优解的状态中，受到伤害最少的
	for(int i = 0 ; i <= m-1 ; i ++){
		if(dp[n][i] == ans1){
			ans2 = i;
			break;
		}
	}
	cout<<ans1<<" "<<m-ans2;
	return 0;
}

1020 潜水员

潜水员下潜的深度需要各种数量的氧和氮。

潜水员有一定数量的气缸，每个气缸都有重量和两种的气体容量。

求最少需要的气缸重量。

题解

这里把氧气、氮气需求当作dp的两个状态，求至少满足这两个需求量下的最少气缸容量。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 105;
const int maxm = 105;

int n,m,k,dp[maxn][maxm];

int main(void){
	cin>>n>>m>>k;
	memset(dp,inf,sizeof(dp));
	dp[0][0] = 0;
	for(int i = 1 ; i <= k ; i ++){
		int a,b,c; cin>>a>>b>>c;
		for(int j = n ; j >= 0 ; j --){
			for(int r = m ; r >= 0 ; r --){
				dp[j][r] = min(dp[j][r], dp[max(0,j-a)][max(0,r-b)] + c);
			}
		}
	}
	cout<<dp[n][m];
	return 0;
}

1013 机器分配

一共有M台相同的设备，准备分给下属的 N 个分公司。

现在，给定矩阵N*M，表示给 第 i 个 公司分配 j 个机器时的盈利，求最大总盈利。

题解

相当于是分组背包问题，我们为每个公司选择一个方案；

每个公司的状态只能从上一个公司转移过来；

最后，用dfs回溯状态；

注意：不是多重背包问题，因为对于每个公司而言，题目只给了几个机器累计的盈利，方案无法叠加。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
using namespace std;
const int maxn = 100;
const int maxm = 100;

int n,m;
int b[maxn][maxm],dp[maxn][maxm],ans[maxn];

void dfs(int i, int j){
	if(i == 0) return;
	for(int t = 0 ; t <= j ; t ++){
		if(dp[i-1][j-t] + b[i][t] == dp[i][j]){
			ans[i] = t;
			dfs(i-1,j-t);
			return;
		}
	}
}

int main(void){
	cin>>n>>m;
	for(int i = 1 ; i <= n ; i ++){
		for(int j = 1 ; j <= m ; j ++){
			cin>>b[i][j];
		}
	}
	for(int i = 1 ; i <= n ; i ++){
		for(int j = m ; j >= 0 ; j --){
			for(int r = 0 ; r <= j ; r ++){
				dp[i][j] = max(dp[i-1][j-r] + b[i][r], dp[i][j]);
			}
		}
	}
	cout<<dp[n][m]<<"\n";
	dfs(n,m);
	for(int i = 1 ; i <= n ; i ++){
		cout<<i<<" "<<ans[i]<<"\n";
	}
	return 0;
}

487 金明的预算方案

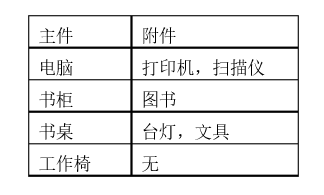
现在有M元钱和N个物品，如果要买归类为附件的物品，必须先买该附件所属的主件。

每个主件可以有0-2个附件，附件不再有从属于自己的附件。

现在给定每个物品的价格w和价值v，要求最多获得物品的总价值。

题解

这题如果用树上DP的模板求解，处理每个节点的时间复杂度为\(O(M*M)\)，总的时间复杂度约为\(O(N*M*M)\)，因为M <= 32000，所以会超时。

注意到，每个附件不再有从属于自己的附件，且<=2个，因此，我们可以将每个主件及其附件看作是一个分组，优化为分组背包问题。分组背包 + 二进制优化枚举 的总时间复杂度为\(O(N_{分组数}*M)\)，不会超时。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<bits/stdc++.h>
using namespace std;
const int maxn = 100;
const int maxm = 40000;

int n,m,f;
int w[maxn],v[maxn],dp[maxm];
bool nd[maxn];
vector<int > g[maxn];

int main(void){
	cin>>m>>n;
	for(int i = 1 ; i <= n ; i ++){
		cin>>w[i]>>v[i]>>f;
		v[i] = w[i]*v[i];
		if(f != 0) g[f].push_back(i);
		else nd[i] = true; // 若没有父节点，则为主件
	}
	for(int i = 1 ; i <= n ; i ++){
		for(int j = m ; j >= 0 ; j --){
			if(!nd[i]) continue; // 若不是主件，则跳过
			int siz = g[i].size(); // 二进制枚举分组内的每一个选择，并更新DP状态
			for(int s = 0 ; s < (1<<siz) ; s ++){
				int v_sum = v[i];
				int w_sum = w[i];
				for(int t = 0 ; t < siz ; t ++){
					if((s>>t) & 1){
						v_sum += v[g[i][t]];
						w_sum += w[g[i][t]];
					}
				}
				if(j >= w_sum) dp[j] = max(dp[j], dp[j-w_sum] + v_sum);
			}
		}
	}
	cout<<dp[m];
	return 0;
}

10 有依赖的背包问题

有 N 个物品和一个容量是 V 的背包。

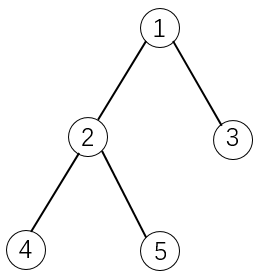
物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：

将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大？输出最大价值。

题解

树形DP - 陈志伟的个人博客

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<bits/stdc++.h>
using namespace std;
const int maxn = 105;
const int maxm = 105;

int n,m;
int w[maxn],v[maxn],dp[maxn][maxm],p,r;
vector<int > e[maxn];

void dfs(int x){
	for(auto it : e[x]){
		dfs(it);
	}
	for(auto it : e[x]){
		for(int j = m ; j >= 0 ; j --){
			for(int k = 0 ; j-k >= w[x]; k ++){
				dp[x][j] = max(dp[x][j], dp[x][j-k] + dp[it][k]);
			}
		}
	}
}

int main(void){
	cin>>n>>m;
	for(int i = 1 ; i <= n ; i ++){
		cin>>w[i]>>v[i]>>p;
		if(p != -1) e[p].push_back(i);
		else r = i;
        // 注意这里的初始化 不能只是 dp[i][w[i]] = v[i];
        // 而是要将w[i] - m 置为 v[i]
        // 否则，若有m剩余，则dp[r][m]不是最优解
		for(int j = w[i] ; j <= m ; j ++){
			dp[i][j] = v[i];
		}
	}
	dfs(r);
	cout<<dp[r][m];
	return 0;
}

11 背包问题求方案数

在01背包的基础上，要求输出 最优解的方案数（答案需要模 109+7）。

题解

为了求解最优解的方案数（区分同数值的不同下标），我们需要设置一个\(cnt[i][j]\)数组来记录：

考虑前1-i 个物品，背包容量为j时最优解（\(dp[i][j]\)）的方案数。

这里的cnt数组需要进行初始化。\(cnt[0][j]\)表示考虑0个物品的最优解方案数，此时无论背包容量j为多少，方案树都为1。

  • 这里的cnt和dp一样，也可以进行一维数组的优化。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
const int maxn = 1e3 + 5;
const int maxm = 1e3 + 5;

int n,m;
int dp[maxm],cnt[maxm];

int main(void){
	cin>>n>>m;
	for(int i = 0 ; i <= m ; i ++){
		cnt[i] = 1;
	}
	for(int i = 1 ; i <= n ; i ++){
		int w,v; cin>>w>>v;
		for(int j = m ; j >= w ; j --){
			if(dp[j-w] + v > dp[j]){
				dp[j] = dp[j-w] + v;
				cnt[j] = cnt[j-w]; //拿
			}else if(dp[j-w] + v == dp[j]){
				cnt[j] = (cnt[j] + cnt[j-w])%mod; // 拿+不拿
			}
		}
	}
	cout<<cnt[m];
	return 0;
}

12 背包问题求具体方案

在01背包的基础上，要求输出 字典序最小的最优方案。

这里的字典序是指：所选物品的编号所构成的序列。物品的编号范围是 1…N。

题解

为了输出01背包最优解的方案，我们需要在DP的状态转移进行回溯；

每个DP状态对应一个决策：对物品i 选/不选；

但是，当我们从1-N进行DP转移后，我们只能从后向前进行回溯，无法得到字典序最小的方案；

字典序最小要求：对物品1-N 从前往后 进行决策，若选/不选 都能到达最优解，那么优先选。

因此，我们需要设置\(dp[i][j]\)为考虑n-i个物品，容量为j时的最大价值。

最后，进行回溯得到路径即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1050;
const int maxm = 1050;

int n,m;
int dp[maxn][maxm],w[maxn],v[maxn];
vector<int > path;

void dfs(int i, int j){
	if(i == n+1) return;
	if(j >= w[i] && dp[i][j] == dp[i+1][j-w[i]] + v[i]){
		path.push_back(i);
		dfs(i+1,j-w[i]);
	}else{
		dfs(i+1,j);
	}
}

int main(void){
	cin>>n>>m;
	for(int i = 1 ; i <= n ; i ++){
		cin>>w[i]>>v[i];
	}
	for(int i = n ; i >= 1 ; i --){
		for(int j = m ; j >= 0 ; j --){
			if(j >= w[i]) dp[i][j] = max(dp[i+1][j], dp[i+1][j-w[i]] + v[i]);
			else dp[i][j] = dp[i+1][j];
		}
	}
	dfs(1,m);
	for(auto it : path){
		cout<<it<<" ";
	}
	return 0;
}

734 能量石

吃完第 i 块能量石需要花费的时间为 Si 秒。第 i 块能量石最初包含 Ei 单位的能量，并且每秒将失去 Li 单位的能量。能量石中包含的能量最多降低至 0。开始吃一块能量石时，他就会立即获得该能量石所含的全部能量。

吃能量石可以获得的最大能量是多少？

题解

我们先假设一个较小的贪心问题：

若只有2个能量石A,B，那么应该先吃哪个？当满足下面这个式子时，先吃A更优，因为总损失更小。 \[ A + B - A.w*B.l > B + A - B.w*A \\ \] 即： \[ A.w*B.l < B.w*A \] 同理，不满足时，先吃B更优。

对应n个能量石，就是多个该子问题的重叠。我们使用该规则进行排序，可以得到吃能量石的优先级。

最后，根据这个顺序进行01背包的求解即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
using namespace std;
const int maxn = 105;
const int maxm = 1e4;

struct stone{
	int w,v,l;
	bool operator<(const stone & rhs){
		return w*rhs.l < rhs.w*l;
	}
}s[maxn];

int dp[maxm];
int t,n,ans,sum;

void solve(int c){
	ans = sum = 0;
	memset(dp,0,sizeof(dp));
	cin>>n;
	for(int i = 1 ; i <= n ; i ++){
		cin>>s[i].w>>s[i].v>>s[i].l;
		sum += s[i].w;
	}
	sort(s+1,s+1+n);
	for(int i = 1 ; i <= n ; i ++){
		for(int j = sum ; j >= 0 ; j --){
			int now_v = s[i].v - s[i].l*(j-s[i].w);
			if(j >= s[i].w && now_v >= 0){
				dp[j] = max(dp[j], dp[j-s[i].w] + now_v);
			}
			ans = max(dp[j],ans);
		}
	}
	cout<<"Case #"<<c<<": "<<ans<<"\n";
	return;
}

int main(void){
	cin>>t;
	for(int i = 1 ; i <= t ; i ++){
		solve(i);
	}
	return 0;
}
题解 > AcWing > 动态规划
#动态规划 #AcWing
AcWing算法提高课：动态规划3-背包模型
https://czwcugb.github.io/题解/acwing-advance/AcWing-DP-3/
作者
ChenZhiwei
发布于
2025年2月7日
许可协议