GPLT团体程序设计天梯赛模拟：2025年校赛

GPLT团体程序设计天梯赛模拟：2025年校赛

摘要

题目 分值 知识点
竞赛 10 容斥原理
盒子游戏 15 博弈论
游戏机前的队伍 25 模拟、数据结构
国家管理 25 DFS
灯 25 二分答案
科技树 30 树上背包

L4 竞赛

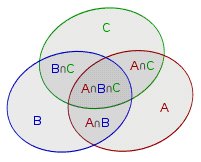
Alice的班级有50名学生参与三种学科竞赛：数学、物理和化学。已知：

  • 参加数学竞赛的有25人，物理竞赛28人，化学竞赛20人；
  • 同时参加数学和物理的有12人，同时参加数学和化学的有8人，同时参加物理和化学的有10人；
  • 同时参加所有三种竞赛的有5人。

问题：

  1. 至少参加一项竞赛的学生有多少人？
  2. 恰好参加两种竞赛的学生有多少人？

Alice很快解决了该问题，于是其他班级的同学也向Alice求助，请你写个程序来自动解决这类问题：给出8个数字，分别代表学生总数 n 、数学竞赛的人数 a 、参加物理竞赛的人数 b 、参加化学竞赛的人数 c 、同时参加数学和物理的人数 ab 、同时参加数学和化学的人数 *a**c* 、同时参加物理和化学的人数 *b**c* 、同时参加所有三种竞赛的人数 *ab**c* ，问至少参加一项竞赛的学生有多少人？恰好参加两种竞赛的学生有多少人？

输入格式：

输入一行，给出八个均不超过 100 的整数 n,a,b,c,ab,ac,bc,*ab**c* ，含义同题目描述。

输出格式：

在一行中输出用空格间隔的两个正整数 ans1,ans2 ，其中 ans1 代表至少参加一项竞赛的学生人数，ans2 代表恰好参加两种竞赛的学生人数。

输入样例：

1
50 25 28 20 12 8 10 5

输出样例：

1
48 15

题解：

1
2
3
4
5
6
7
8
9
10
11
#include<bits/stdc++.h>
using namespace std;

int n,a,b,c,ab,ac,bc,abc;

int main(void){
	cin>>n>>a>>b>>c>>ab>>ac>>bc>>abc;
	cout<<a+b+c - ab - ac - bc + abc<<" ";
	cout<<(ab+bc+ac - 3*abc);
	return 0;
}

L5 盒子游戏

有两个相同的盒子，其中一个装了 n 个球，另一个装了一个球。 Alice 和 Bob 发明了一个游戏，规则如下：

Alice 和 Bob 轮流操作， Alice 先操作。每次操作时，游戏者先看看哪个盒子里的球的数目比较少（数量相同就随便选一个盒子）， 然后清空这个盒子（盒子里的球直接扔掉），然后把另一个盒子里的球拿一些到这个盒子中，使得两个盒子都至少有一个球。如果一个游戏者无法进行操作（无法使得两个盒子都至少有一个球），他（她）就输了。下面一行是一个 n=6 的游戏：

Alice先操作，分为 (3,3) Bob操作，丢弃 3 ，剩下 3 ，分为 (1,2) Alice操作，丢弃 1 ，剩下 2 ，分为 (1,1) Bob操作， 丢弃 1 ，剩下 1 Bob 无法继续操作，因此 Alice 获胜。

你的任务是找出谁会获胜。假定两人都很聪明，总是采取最优策略。

输入格式：

输入最多包含 300 组测试数据。每组数据仅一行，包含一个整数 n (2≤n≤109) 。输入结束标志为 n=0 。

输出格式：

对于每组数据，输出胜者的名字。

输入样例：

1
2
3
4
2
3
4
0

输出样例：

1
2
3
Alice
Bob
Alice

题解：

根据题意， 谁先拿到1，无法分解就lose。

n = 1，Alice(1) lose

n = 2，Alice(2) -> Bob(1) win

n = 3，Alice(3) -> Bob(2) -> Alice(1) lose

n = 4，Alice(4) -> Bob(3) win

这里4一定分解为3,1。若将4分解为2,2，Bob拿到2，Alice就会输；若将4分解为3,1，Bob拿到3，根据n=3的结果，先拿到3的人将lose，所以Alice是必胜；

根据上述情况递推，可以得到 1，3，7，15的情况【2^n - 1】，Alice会输，否则会赢。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<bits/stdc++.h>
using namespace std;
set<int > st;

int main(void){
	int t = 2;
	while(t <= 1e9){
		st.insert(t-1);
		t *= 2;
	}
	int x;
	while(cin>>x, x){
		if(st.count(x)){
			cout<<"Bob\n";
		}else{
			cout<<"Alice\n";
		}
	}
	return 0;
}

M1 游戏机前的队伍

补充说明：这里的排队和传统的排队有出入。正在游玩的人为队列的前两位，所以正在游玩视为正在排队。

机厅里有一台游戏机，每次可供最多两人同时游玩。但是来玩的人显然不止两个！这个时候他们就需要排队了，而你需要写一个程序维护这个队列，并在他人游玩结束后通知接下来上场的人。在整个过程中，有以下几种事件可能发生：

  • start：一局游戏开始。若这不是第一局游戏，则上一局的参与者在这一局游戏开始前一瞬间按照原本的顺序回到队尾。此时你应该按在队列中的顺序输出这一局上场的人的名字（正常来讲是队列前两位或者唯一一个人），若有两个则以空格分割。若这一局无人上场，则输出 Error 并忽略这条事件。
  • arrive x：x 到达机厅并且将自己加入队尾，此时 x 不应该在排队，否则输出 Error 并忽略这条事件。若该事件成功执行则输出 OK。
  • leave x：x 离开机厅并离开队列。此时 x 应该在排队但不应该在游玩，否则输出 Error 并忽略这条事件。若该事件成功执行则输出 OK。

你需要维护队列信息，并输出上述事件中要求的输出。

输入格式

第一行一个整数 n(1≤n≤1e5)，表示事件条数。

接下来 n 行，每行表示一条事件。

输出格式

按照题目要求输出 n 行，表示程序对事件的响应。

输入样例1：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14
start
arrive A
start
arrive B
arrive C
arrive D
start
leave C
leave D
start
arrive A
arrive D
leave E
start

输出样例1：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Error
OK
A
OK
OK
OK
B C
Error
OK
A B
Error
OK
Error
C D

输入样例2：

1
2
3
4
3
arrive A
arrive B
arrive C

输出样例2：

1
2
3
OK
OK
OK

说明/提示

【样例说明】

样例 1 中发生了如下的事件：

  • 第一次 start 时队列并没有任何人，输出 Error。
  • A 随即加入队列。
  • 第二次 start 时仅有 A 一个人，所以输出 A。
  • B, C, D 随即依次加入队列。
  • 第三次 start 时 B, C 上场。
  • C 试图离开，但是他在游玩。所以输出 Error。
  • D 成功离开。
  • 第四次 start 时 A, B 上场。
  • A 试图加入队列，但是他已经在队列中。输出 Error。
  • D 重新加入队列。
  • E 试图离开，但是他根本不在排队，输出 Error。
  • 第五次 start 时 C, D 上场。

样例 2 中，A, B, C 依次入队，操作合法，输出三个 OK。

题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<bits/stdc++.h>
using namespace std;
const string def = "$$$$$$$";

deque<string > q; // 使用双端队列的原因是，相比queue, 可以使用erase函数，不用每次遍历整个队列
map<string , bool> mp; // 1 - 在排队，且在game； 0 - 在排队，但不在game； mp.count(x) = 0 - 不在排队 
string g[3]; // g[1], g[2] - 正在排队的2人；
int t;

void Erase_queue(deque<string > & q, string re){
	for(auto it = q.begin() ; it != q.end() ; ++it){
		if(*it == re){
			q.erase(it);
			break;
		}
	}
}

void solve(void){
	string op; cin>>op;
	if(op == "start"){
		if(g[1] != def){
			q.push_back(g[1]); mp[g[1]] = 0;
		}
		if(g[2] != def){
			q.push_back(g[2]); mp[g[2]] = 0;
		}
        // 这里要先把在游戏2人加入队尾，再判断队列长度，否则会出错。
		if(q.empty()){
			cout<<"Error"<<"\n"; return;
		}else if(q.size() == 1){
			g[1] = q.front(); q.pop_front();
			g[2] = def;
			mp[g[1]] = 1;
			cout<<g[1]<<"\n";
		}else{
			g[1] = q.front(); q.pop_front();
			g[2] = q.front(); q.pop_front();
			mp[g[1]] = mp[g[2]] = 1;
			cout<<g[1]<<" "<<g[2]<<"\n";
		}
	}else if(op == "arrive"){
		string name;cin>>name;
		if(mp.count(name)){
			cout<<"Error"<<"\n"; return;
		}
		cout<<"OK"<<"\n";
		mp[name] = 0;
		q.push_back(name);
	}else if(op == "leave"){
		string name;cin>>name;
		if(!mp.count(name)){
			cout<<"Error"<<"\n"; return;
		}
		if(mp.count(name) && mp[name] == 1){
			cout<<"Error"<<"\n"; return;
		}
		cout<<"OK"<<"\n";
		mp.erase(name);
		Erase_queue(q, name);
	}
}

int main(void){
	cin>>t;
	g[1] = g[2] = def;
	while(t--){
		solve();
	}
	return 0;
}

M2 国家管理

Alice 所在的国家中的城市通过道路连接起来，形成一颗树（全连通但无环），并且每个城市分为红派或者蓝派。

相邻的同派城市可以形成一个城市群，一个同派的城市群距离首都越远，并且城市群内的城市越多，对国家的威胁越大。

我们将一个城市群的威胁值表示为 一个城市群内距离首都距离最近的城市相对于首都的距离 加上 城市群内城市的数量 。

我们给城市编号 1 到 n，并假设首都的编号为 1 。

道路的长度均为 1 。

总统委托 Alice 计算最大威胁值的城市群的威胁值为多少，你能写一个程序来帮帮她吗？

输入格式：

第一行给出一个整数 n (1≤n≤1e5) ，代表城市的总数。

第 2 到 n 行，每行给出两个整数 u 和 v ，代表编号为 u 的城市与编号为 v 的城市有道路相连（保证所给的图能形成一颗树）。

第 n+1 行，给出 n 个小于等于 1 的非负整数 *c**i* ，如果 *c**i=1 代表编号为 i* 的城市为红派， *c**i=0 代表编号为 i* 的城市为蓝派。

输出格式：

输出一个整数，代表最大威胁值的城市群的威胁值为多少。

输入样例：

1
2
3
4
5
6
7
6
1 2
1 3
2 4
2 5
3 6
0 1 1 0 1 0

输出样例：

1
3
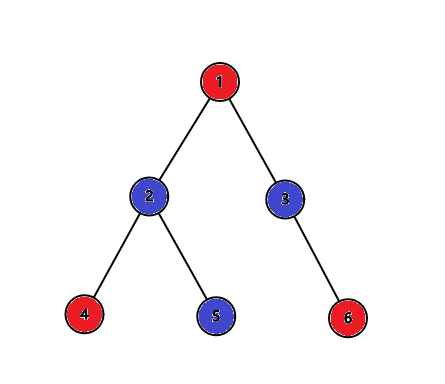
  • 分为五个城市群，{1}，{2,5}，{3}，{4}，{6}
  • 威胁值分别为，1，3，2，3，3
  • 最大值为 3 因此输出 3

题解：

以下两种写法时间上没有差异：

1）两次dfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;

int n;
vector<int > e[maxn];
bool visited[maxn];
int depth[maxn],color[maxn];
int min_, sum, ans;

// 求出每个节点深度
void get_depth(int x){
	for(auto it : e[x]){
		if(it != 1 && depth[it] == 0){
			depth[it] = depth[x] + 1;
			get_depth(it);
		}
	}
}
// 计算相邻同色节点的数量和最小深度
void dfs(int x){
	min_ = min(min_, depth[x]);
	sum++;
	visited[x] = true;
	for(auto it : e[x]){
		if(!visited[it] && color[x] == color[it]){
			dfs(it);
		}
	}
}

int main(void){
	cin>>n;
	for(int i = 1 ; i <= n-1 ; i ++){
		int u, v; cin>>u>>v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	for(int i = 1 ; i <= n ; i ++){
		cin>>color[i];
	}
	get_depth(1);
	for(int i = 1 ; i <= n ; i ++){
		if(!visited[i]){
			min_ = INT_MAX;
			sum = 0;
			dfs(i);
			ans = max(sum + min_, ans);
		}
	}
	cout<<ans;
	return 0;
}

2）单次dfs（更简洁）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;

int n,ans;
int color[maxn],num[maxn];
vector<int > e[maxn];

void dfs(int x, int f, int d){
	num[x] = 1;
	for(auto it : e[x]){
		if(it != f){
			dfs(it, x, d+1);
			if(color[it] == color[x]) num[x] += num[it];
		}
	}
	ans = max(ans, num[x] + d);
}

int main(void){
	cin>>n;
	for(int i = 1 ; i <= n-1 ; i ++){
		int u, v; cin>>u>>v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	for(int i = 1 ; i <= n ; i ++){
		cin>>color[i];
	}
	dfs(1, 0, 0);
	cout<<ans;
	return 0;
}

M3 灯

有 n 盏灯排成一列，其中有些灯开着，有些灯关着。Alice希望灯是错落有致的，他定义一列灯的状态的不优美度为这些灯中最长的连续的开着或关着的灯的个数。小可可最多可以按开关 k 次，每次操作可以使该盏灯的状态取反：原来开着的就关着，反之开着。现在给出这些灯的状态，求操作后最小的不优美度。

输入格式：

第一行两个整数 n,k (1≤k≤n≤2e5)，代表灯的总数为 n ，最多可以按 k 次开关

第二行是一个长度为 n 的字符串，其中有两种字符：N 和 F。其中 N 表示该灯开着，F 表示该灯关着。

输出格式：

输出一个整数，代表操作后最小的不优美度。

输入样例：

1
2
8 1
NNNFFNNN

输出样例：

1
3

题解：

P3718 AHOI2017初中组] alter - 洛谷

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include<bits/stdc++.h>
using namespace std;

int n,k,ans;
string s;

// A.i 号灯修改后和 (i+1) 号灯一样，那么应该修改 (i−1) 号灯。
// B.i 号灯修改后和 (i+1) 号灯不一样，那么就修改 i 号灯。
// 但是对于A，当x==1时， 修改i-1可能会导致前面连成2，需要特判
bool check(int x){
	string t = s;
	int cnt = 1;
	int sum = 0;
	for(int i = 2 ; i <= n ; i ++){
		if(t[i] != t[i-1]){
			cnt = 1;
		}else{
			cnt++;
		}
		if(cnt > x){
			if(i+1 <= n && t[i+1] == t[i]) t[i] = (t[i] == 'N' ? 'F':'N');
			sum++; cnt = 1;
		}
	}
	return sum <= k;
}

int main(void){
	cin>>n>>k;
	cin>>s;
	s = " " + s;
	// 特判 x == 1 是否可行
	int n1 = 0, n2 = 0;
	for(int i = 1 ; i <= n ; i ++){
		if(i % 2 == 0){
			s[i] == 'N' ? ++n1:++n2;
		}else{
			s[i] == 'F' ? ++n1:++n2;
		}
	}
	if(n1 <= k || n2 <= k){
		cout<<1; return 0;
	}
	int l = 1;
	int r = n;
	while(l+1 != r){
		int mid = (l+r)/2;
		if(check(mid)){
			r = mid;
		}else{
			l = mid;
		}
	}
	cout<<r;
	return 0;
}

H1 科技树

如果我们想要解锁某种科技，必须解锁其前置科技，这种前置关系正好形成一棵树。

如果解锁科技 5 ，则必须解锁科技 1 和 2

解锁科技需要资源，同时会给一些科技点，Alice的资源有限，但她希望得到最多的科技点。

每项科技的编号为 i ，需要的资源为 *v**i* ，提供的科技点为 *w**i* ，依赖的科技为 *p**i* 。科技的下标范围是 1...N 。

输出能获得的最多科技点。

输入格式：

第一行有两个整数 N，V，用空格隔开，分别表示科技个数和Alice初始拥有的资源。

接下来有 N 行数据，每行数据表示一个科技。 第 i 行有三个整数 vi,wi,pi，用空格隔开，分别表示解锁科技需要的资源、提供的科技点和依赖的科技编号。 如果 pi=−1 ，表示根节点。 数据保证所有科技构成一棵树。

输出格式：

输出一个整数，代表能获得的最多科技点。

输入样例：

1
2
3
4
5
6
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

输出样例：

1
11

数据范围：

1≤N,V≤100 1≤vi,wi≤100

父节点编号范围：

  • 内部结点：1≤*p**i≤N*;
  • 根节点 *p**i*=−1;

题解：

（树上背包模板）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e3;
const int maxm = 1e3;

int n,m,f,r;
int w[maxn],v[maxn];
int dp[maxn][maxm];
vector<int > e[maxn];

void dfs(int x){
	for(auto it : e[x]){
		dfs(it);
	}
	for(auto it : e[x]){
		for(int j = m ; j >= 0 ; j --){
			for(int k = 0 ; j-k >= w[x] ; k ++){
				dp[x][j] = max(dp[x][j], dp[x][j-k] + dp[it][k]);
			}
		}
	}
}

int main(void){
	cin>>n>>m;
	for(int i = 1 ; i <= n ; i ++){
		cin>>w[i]>>v[i]>>f;
		if(f == -1) r = i;
		else e[f].push_back(i);
		for(int j = w[i]; j <= m ; j ++){
			dp[i][j] = v[i];
		}
	}
	dfs(r);
	cout<<dp[r][m];
	return 0;
}
题解 > GPLT > 校内模拟
#GPLT
GPLT团体程序设计天梯赛模拟：2025年校赛
https://czwcugb.github.io/题解/GPLT/2025-school/
作者
ChenZhiwei
发布于
2025年4月8日
许可协议