树状数组

类型	下标修改	区间和查询
普通数组	\(O(1)\)	\(O(N)\)
前缀和数组	\(O(N)\)	\(O(1)\)
树状数组	\(O(logN)\)	\(O(logN)\)

对于普通数组，区间和查询的复杂度较高；

前缀和数组虽然能优化区间和查询，但是下标修改的复杂度较高；

树状数组是一种居中策略，两种操作复杂度都为O(logN)。

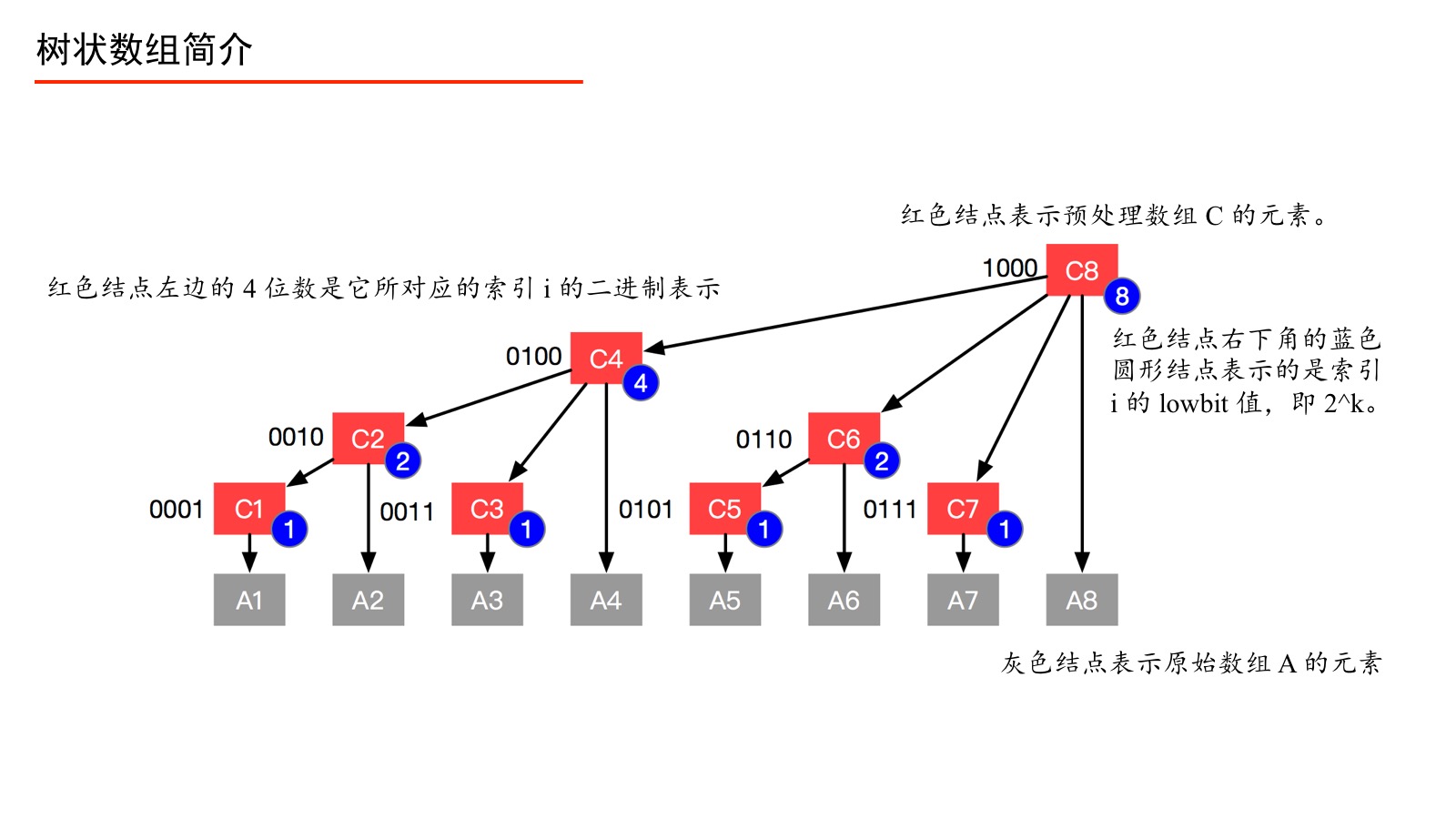
（图片来源：树状数组学习笔记 - AcWing）

设 树状数组 为 c，c[i]表示[i - lowbit(i) + 1, i]区间的和。

1）更新数组：对a[i]更新k，对i 不断加上lowbit(i)，更新每个对应的c[i], 直到上界N；

2）查询区间和： [1, i ]的区间和，依次减去lowbit(i), 直到i等于0即可；

模板题：P3374 【模板】树状数组 1 - 洛谷

#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 10;

int n,m;
int a[maxn],f[maxn]; // 注意a数组不是必要的

int lowbit(int x){
	// return x & (~x + 1)
	return x&(-x);
}

// a[x] += k, 并更新f数组
void update(int x, int k){
	a[x] += k;
	while(x <= n){
		f[x] += k;
		x += lowbit(x);
	}
}

// 求a[1-x]的和
int getSum(int x){
	int res = 0;
	while(x){
		res += f[x];
		x -= lowbit(x);
	}
	return res;
}

void init(){
	cin>>n>>m;
	for(int i = 1 ; i <= n ; i ++){
		int v; cin>>v;
		update(i, v);
	}
}

void solve(){
	int op; cin>>op;
	if(op == 1){
		int x, k; cin>>x>>k;
		update(x, k);
	}else{
		int x, y; cin>>x>>y;
		cout<<getSum(y) - getSum(x-1)<<"\n";
	}
}

int main(void){
	cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
	init();
	while(m--){
		solve();
	}
	return 0;
}