二叉树算法合集

二叉树基本性质

性质1：在二叉树的第 \(i\) 层上至多有 \(2^{i-1}\) 个结点（i>=1）

性质2：深度为 \(k\) 的二叉树至多有 \(2^k-1\) 个结点（k>=1）

性质3：对于任何一颗二叉树T，如果其终端结点数为\(n_0\)，度为2的结点数为\(n_2\)，则\(n_0=n_2+1\)

原理：点数 = 边数 + 1

由 \(n = n0 + n1 + n2 = 2*n2 + n1 + 1\) 得 \(n_0=n_2+1\)

性质4：具有n个节点的完全二叉树深为\(log_2{k}+1\)

性质5：如果对一颗有n个结点的完全二叉树（其深度为\([log_2n]+1\)）的结点按层序编号（从第1层到\([log_2n]+1\)层，每层从左到右），对任一结点i（1<=i<=n）:

（1）如果\(i=1\)，则结点i是二叉树的根，无双亲，如果\(i>1\),则其双亲结点是结点\([i/2]\) （2）如果\(2i>n\)，则结点i无左孩子（结点i为叶子结点）否则左孩子是结点\(2i\)。 （3）如果\(2i+1>n\),则结点i无右孩子，否则其右孩子是结点\(2i+1\).

若根节点从0开始，左 = \(2i + 1\)，右 = \(2i+2\)

节点数据结构

1
2
3
4
5
6
7
8
9
10
11
struct node{
	int val;
	node * l;
	node * r;
	
	node(int val_){
		val = val_;
        l = nullptr;
        r = nullptr;
	}	
};

二叉树的遍历

先序遍历

1
2
3
4
5
6
7
8
9
10
11
12
void preTra(node * p){
	if(p == nullptr) return;
	if(!isMirror){
		pre.push_back(p->val);
		preTra(p->l);
		preTra(p->r);
	}else{
		pre.push_back(p->val);
		preTra(p->r);
		preTra(p->l);
	}
}

中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
void inTra(node * p){
	if(p == nullptr) return;
	if(!isMirror){
		inTra(p->l);
        in.push_back(p->val);
		inTra(p->r);
	}else{
		inTra(p->r);
		in.push_back(p->val);
		inTra(p->l);
	}
}

后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
void postTra(node * p){
	if(p == nullptr) return;
	if(!isMirror){
		postTra(p->l);
		postTra(p->r);
		post.push_back(p->val);
	}else{
		postTra(p->r);
		postTra(p->l);
		post.push_back(p->val);
	}
}

层序遍历

1
2
3
4
5
6
7
8
9
10
11
void layerTra(node * p){
	queue<node *> q;
	q.push(p);
	while(!q.empty()){
		node * f = q.front();q.pop();
		layer.push_back(q->val);
		
		if(f->l != nullptr) q.push(f->l);
		if(f->r != nullptr) q.push(f->r);
	}
}

二叉树的建树

T1--已知后序和中序遍历

1127 ZigZagging on a Tree - PAT (Advanced Level) Practice (pintia.cn)

后序和中序遍历唯一地确定一颗二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
node* create(int postl, int postr, int inl, int inr){
	if(postl > postr) return nullptr;
	
	int i = inl;
	while(i <= inr && in[i] != post[postr]) i++;
	
	node* p = new node(in[i]);
	p->l = create(postl, postl + (i - inl) - 1, inl, i - 1);
    //注意：这里不能改成（r-inl），因为左右子树未必节点数相同
	p->r = create(postl + (i - inl), postr - 1, i + 1, inr);
	
	return p;
}
node * root = create(0, n-1, 0, n-1);

T2--已知先序和中序遍历

前序和中序遍历唯一地确定一颗二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
node* create(int prel, int prer, int inl, int inr){
    if(prel > prer) return nullptr;
    
    int i = inl;
    while(i <= inr && in[i] != pre[prel]) i++;
    
    node * p = new node(in[i]);
    p->l = create(prel+1, prel + (i-inl), inl, i-1);
    p->r = create(prel + (i-inl) + 1, prer, i+1, inr);
    
    return p;
}
node * root = create(0, n-1, 0, n-1);

T3--已知层序和中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
node* create(int layerl, int layerr, int inl, int inr){
	if(layerl > layerr){
		return nullptr;
	}else{
		int i = inl;
		while(i <= inr && in[i] != layer[layerl]) i++;
		
		node *p = new node(in[i]);
		p->l = create(layerl+1, layerl + (i-inl) ,inl, i-1);
		p->r = create(layerl+(i-inl)+1, layerr, i+1, inr);
		return p;
	}
}

T4--已知先序和后序遍历（不唯一）

1119 Pre- and Post-order Traversals - PAT (Advanced Level) Practice (pintia.cn)

已知先序和后序遍历可能无法唯一地确定二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
node* create(int prel, int prer, int postl, int postr){
	if(prel == prer){
		node *p = new node(pre[prel]);
		return p;
	}else{
		node *p = new node(pre[prel]);
		int i = prel+1;
		while(i <= prer && pre[i] != post[postr-1]) i++;//找到后序遍历倒数第二个点，即右子树的第一个点
		if(i - prel - 1 > 0){ 
			p->l = create(prel+1, i-1, postl, postl+(i-prel-1)-1);
		}else{ //若左子树为空，那么右子树第一个点可能在左子树，也可能在右子树。此处我们将该点放在右子树
			Unique = false;
		}
		p->r = create(i, prer, postl+(i-prel-1), postr-1);
		return p;
	}
}
node * root = create(0, n-1, 0, n-1);

序列互转

任意两种序列 转 其他

若题目只要求某个遍历序列，可以在建树的过程中，直接生成序列。

先 + 中 转 后

1138 Postorder Traversal - PAT (Advanced Level) Practice (pintia.cn)

1
2
3
4
5
6
7
8
void getPost(int prel, int prer, int inl, int inr){
	if(prel > prer) return;
	int i = inl;
	while(i <= inr && in[i] != pre[prel]) i++;
	getPost(prel+1, prel + (i-inl), inl, i-1);
	getPost(prel+(i-inl)+1, prer, i+1, inr);
	post.push_back(pre[prel]);
}

先+后 转 中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void getIn(int prel, int prer, int postl, int postr){
	if(prel == prer){
		in.push_back(pre[prel]);
		return;
	}
	if(pre[prel] == post[postr]){
		int i = prel+1;
		while(i <= prer && pre[i] != post[postr-1]) i++;
		if(i - prel > 1){
			getIn(prel+1, i-1, postl, postl+(i-prel-1)-1);
		}else{
			Unique = false;
		}
		in.push_back(pre[prel]);
		getIn(i, prer, postl+(i-prel-1), postr-1);
	}
}

先/中/后序 转 层序（完全二叉树）

完全二叉树(Complete Binary Tree)：设二叉树的深度为h，除第 h 层外，其它各层 (1~h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

满二叉树(Full binary tree)：各层 (1~h-1) 的结点数都达到最大个数的二叉树。所有节点的度要么为0，要么为2，且所有的叶子节点都在最后一层。

1064 Complete Binary Search Tree - PAT (Advanced Level) Practice (pintia.cn)、

对于一颗完全二叉树/满二叉树而言，按层序从上到下，从左到右地标注（root = 0），可以得到任意一个节点r，其左孩子为r*2+1，右孩子为 r*2 + 2。可以根据这个性质，将先/中/后序序列转为层序。

这里以中序转层序（节点数为n）为例，函数如下：

1
2
3
4
5
6
void inToLayer(int r){
	if(r >= n) return;
	inToLayer(r*2 + 1);
	layer[r] = in[idx++];
	inToLayer(r*2 + 2);
}

层序 转 先/中/后序（完全二叉树）

以 层序 转 后序为例

1
2
3
4
5
6
void postTra(int r){
	if(r >= n) return;
	postTra(r*2 + 1);
	postTra(r*2 + 2);
	post.push_back(layer[r]);
}

求二叉树的深度

1
2
3
4
int getDepth(node * p){
	if(p == NULL) return 0;
	else return 1 + max(getDepth(p->l),getDepth(p->r));
}

求二叉树的镜像

1
2
3
4
5
6
7
8
void mirror(node * p){
	if(p == nullptr) return;
	if(p->l != nullptr || p->r != nullptr){
		swap(p->l, p->r);
		mirror(p->l);
		mirror(p->r);
	}
}

平衡二叉树

定义：一棵空树 或 左右子树的高度差不超过1且左右子树也是平衡树

输入一颗二叉树，判断是否为平衡二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool isBanlance(node * p, int & depth){
	if(p == nullptr){
		depth = 0;
		return true;
	}
	int ld,rd;
    //先判断左右子树是否平衡，再判断当前子树，避免重复计算深度
	if(isBanlance(p->l,ld) && isBanlance(p->r,rd)){
		int diff = abs(ld - rd);
		if(diff <= 1){
			depth = max(ld,rd) + 1;
			return true;
		}
	}
	return false;
}

对称二叉树

定义：一颗二叉树，所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。

直观理解：从根节点画一条纵轴，左右子树完全沿轴对称

核心思想：左右子树对称 <=> 左右根节点相等 && 左子树的左子树和右子树的右子树对称 && 左子树的右子树和右子树的左子树对称

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool isSym(node * le, node * ri){
	if(le == nullptr && ri == nullptr){
		return true;
	}else if(le != nullptr && ri != nullptr){
		return (le->x == ri->x) && isSym(le->l,ri->r) && isSym(le->r,ri->l);
	}else{
		return false;
	}
}

bool isTreeSym(node * p){
	if(p == NULL) return true;
	return isSym(p->l, p->r);
}

完全二叉树

1110 Complete Binary Tree - PAT (Advanced Level) Practice (pintia.cn)

完全二叉树(Complete Binary Tree)：设二叉树的深度为h，除第 h 层外，其它各层 (1~h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

一颗树是完全二叉树的充要条件是：层序遍历的最大下标等于 n-1 (root == 0)

root == 1时，层序遍历的最大下标等于 n

1
2
3
4
5
6
7
8
9
10
11
12
13
bool isComplete(){
	queue<pair<int,int>> q;
	q.push({root, 0});
	while(!q.empty()){
		int f = q.front().first;
		int d = q.front().second;
		q.pop();
		maxIdx = max(maxIdx,d);
		if(nodes[f].l != -1) q.push({nodes[f].l,2*d + 1});
		if(nodes[f].r != -1) q.push({nodes[f].r,2*d + 2});
	}
	return maxIdx == n-1;
}

二叉搜索树BST

二叉搜索树(Binary Search Tree)：它是一棵空树，或者是具有下列性质的二叉树：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

左、右子树也分别为二叉排序树。

一个重要性质：二叉搜索树的中序遍历序列是有序上升的。（很多题目中可利用该性质将BST当成普通二叉树来做）

BST建树

1115 Counting Nodes in a Binary Search Tree - PAT (Advanced Level) Practice (pintia.cn)

1
2
3
4
5
6
7
8
9
10
node * insert(node * p, int x){
	if(p == nullptr){
		p = new node(x);
	}else if(x >= p->val){ //根据不同题目，这里可能是x > p->val
		p->r = insert(p->r, x);
	}else{
		p->l = insert(p->l, x);
	}
	return p;
}
1
2
3
4
5
node * root = nullptr;
for(int i = 0 ; i < n ; i ++){
    cin>>v[i]; //按固定顺序插入的二叉搜索树是唯一的。
    root = insert(root, v[i]);
}

BST上LCA

1143 Lowest Common Ancestor - PAT (Advanced Level) Practice (pintia.cn)

BST上任意两点的最近公共祖先满足条件：\(min(u,v) <= a <= max(u,v)\)

满足这个条件的点是唯一的，是充要条件。

1
2
3
4
5
6
7
8
//沿先序遍历路径找LCA
for(int i = 0 ; i < n ; i ++){
    //pre[i] >= min(u,v) && pre[i] <= max(u,v)
    if((pre[i] >= u && pre[i] <= v) || (pre[i] >= v && pre[i] <= u)){
        a = pre[i];
        break;
    }
}

判断某个先序序列是否来自BST

1043 Is It a Binary Search Tree - PAT (Advanced Level) Practice (pintia.cn)

法1：按该先序序列逐个插入节点，建立BST，与正确的先序序列比较。

法2：直接在先序序列上判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//对于二叉搜索树的先序遍历的序列而言
//头节点一定为根节点，而左右子树的根，在该序列中的距离一定为1
//由此规律可构造的平衡树的节点个数一定是n个
void getPost(int l, int r){
	if(l > r) return;
	int i = l + 1;
	int j = r;
	if(!isMirror){
		while(i <= r && pre[i] < pre[l]) i++;//第一个 >= root的节点
		while(j > l && pre[j] >= pre[l]) j--;//最后一个 < root的节点
	}else{
		while(i <= r && pre[i] >= pre[l]) i++;//第一个 < root的节点
		while(j > l && pre[j] < pre[l]) j--;//最后一个 >= root的节点
	}
	if(i - j != 1) return;
	getPost(l+1, j);
	getPost(i, r);
	post.push_back(pre[l]);
}

平衡二叉搜索树AVL

AVL树的名字来源于它的发明作者G.M. Adelson-Velsky 和 E.M. Landis。

AVL树是最先发明的自平衡二叉查找树（Self-Balancing Binary Search Tree, 简称平衡二叉树）

将二叉树上节点的左子树高度减去右子树高度的值称为该节点的平衡因子BF(Balance Factor)。

每次查找AVL树中的元素，耗时O（logN）

AVL树满足以下两个条件：

条件一：它必须是二叉查找树。

条件二：每个节点的左子树和右子树的高度差至多为1。

AVL建树

1123 Is It a Complete AVL Tree - PAT (Advanced Level) Practice (pintia.cn)

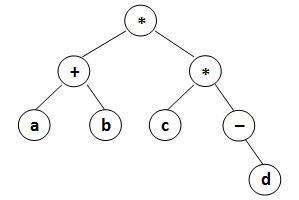
中缀表达式

1130 Infix Expression - PAT (Advanced Level) Practice (pintia.cn)

infix1.JPG

二叉运算树的中序遍历，恰是一个中缀表达式

1
2
3
4
5
6
7
8
9
10
11
string inTra(int p){
	if(p == -1) return "";
	string le = inTra(tree[p].l);
	string ri = inTra(tree[p].r);
	if((le != "" || ri != "") && p != root){ //若非根节点p，存在孩子，需要加上括号
		le = "(" + le;
		ri = ri + ")";
	}
	return le + tree[p].s + ri;
}
cout<<inTra(root);

最优二叉查找树

7-5 最优二叉查找树 - 练习3-2 (pintia.cn)

假设 一颗 查找树 上的每个点（深度为 c ）都有一个查找概率p，那么我们可以得到查找次数的期望： \[ E(c) = \sum_{i}^{n} c_i*p_i \] 最优二叉查找树 指的是 使得查找次数期望最小 的 二叉查找树。

设C（i，j）为以i为左端点，j为右端点的二叉树的查找期望代价。

我们可以得到如下的状态转移方程： \[ \begin{cases} C[i][j] = 0 & i > j \\ C[i][j] = P_i & i = j \\ C[i][j] = min( C[i][k-1] + C[k+1][j] + \sum_{i}^{j} P ) ) & else \\ \end{cases} \] 在得到c[i][j]数组的同时，我们需要可以记录一下，取最小值时候的根k，得到R[i][j]数组，以构造查找树。

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void dp(int x, int y){ //处理坐标为x，y的点
	int res = 0x3f3f3f3f;
	// int root = 0;
	int sum = 0;
	for(int i = x ; i <= y ; i ++){
		sum += c[i][i];
	}
	for(int k = x ; k <= y ; k ++){
		if(sum + c[x][k-1] + c[k+1][y] < res){
			res = sum + c[x][k-1] + c[k+1][y];
			// root = k;
		}
	}
	c[x][y] = res;
	// r[x][y] = root;
}

按主对角线方向进行dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
cin>>n;
for(int i = 1 ; i <= n ; i ++){
    double p;cin>>p;
    c[i][i] = p*10000; // 这题要求输出结果x10000后的数值
    r[i][i] = i;
}
int x = 1,y = 2,cnt = 2;
while( !( x == 1 && y == n) ){
    dp(x, y);
    x++;y++;
    if(y > n){
        x = 1;
        y = ++cnt;
    }
}dp(x, y);
cout<<c[1][n];
笔记 > 数据结构
#数据结构
二叉树算法合集
https://czwcugb.github.io/算法/数据结构/二叉树算法合集/
作者
ChenZhiwei
发布于
2025年1月12日
许可协议